Un algoritmo no supervisado aplicado a la segmentación de
imágenes
Berns, Daniel Walther
UNPSJB, Facultad de Ingeniería
https://www.orcid.org/0000-0002-7231-6392
dwberns@ing.unp.edu.ar
Resumen:
En este trabajo mostramos un algoritmo no
supervisado para segmentar imágenes, basado en la clasificación de
pixeles mediante una red neuronal arbitraria cuyos coeficientes
pueden ser calculados mediante la descomposición en valores
singulares de una matriz. Proveemos un demo publicado en
huggingface, y la teoría respectiva.
Palabras
claves: Segmentación, Imagen, Algoritmo.
A non supervised algorithm for
images segmentation |
Resumen:
In this work we show an unsupervised
algorithm to segment images, based on the classification of pixels
by means of an arbitrary neural network whose coefficients can be
calculated by decomposing a matrix into singular values. We
provide a demo posted on huggingface, and the respective theory.
Keywords:
Segmentation, Image, Algorithm.
Introducción
La segmentación de una imagen digital (ver (Papers With Code | Image
Segmentation, 2022)) es su división en partes con
características distintivas determinadas. Esta tarea tiene múltiples
aplicaciones en medicina (ver (Ronneberger
., 2015), (Ramesh ., 2021), (Liu ., 2021)),
sensado remoto (ver (Kotaridis y
Lazaridou, 2021) y (Jurado ., 2022)),
control de tráfico vehícular (ver (L. Li .,
2018)),
conteo de instancias (ver (Ren y Zemel,
2017) y (Waqas Zamir ., 2019)),
y
navegación de vehículos autónomos (ver (Treml
., 2016) y (Papadeas ., 2021)).
Además, es posible obtener diferentes tipos de resultado. En la
tarea de segmentación semántica se diferencian clases de objetos
(personas, autos, edificios, zonas geográficas, condiciones
climáticas, etc), mediante la clasificación de pixeles de acuerdo
a categorías y regiones de la imagen, pero no se diferencian
instancias de objetos (ver el trabajo sobre imágenes médicas de (Ronneberger ., 2015) y el modelo de
(Wang ., 2022)). En la tarea de
segmentación por instancias (ver Wei
. (2022) y (Ke ., 2021)), se busca
distinguir distintos objetos dentro de una misma categoría. En la
segmentación panóptica (ver (Kirillov
., 2019) y (Xiong ., 2019)),
es posible distinguir entre diferentes clases e instancias y se
unifican las tareas de segmentación semántica y de instancias.
En orden cronológico, tenemos diferentes algoritmos de
segmentación: por agrupamiento (ver (Coleman
y Andrews, 1979)), por "divisorias de aguas" (ver (Beucher, 1992)), por umbral
(ver (Cheriet ., 1998)), por
crecimiento de regiones (ver (Shih y
Cheng, 2005)), por detección de bordes (ver (Muthukrishnan y Radha, 2011)),
y con redes neurales profundas (deep learning neural networks) ((Badrinarayanan ., 2017), (Minaee ., 2021)).
Los algoritmos en uso actualmente, basados en redes neurales
profundas, pueden consultarse en el sitio paperswithcode.com,
en las páginas Papers
with code | semantic segmentation (2022), Papers with code |
instance segmentation (2022) y Papers with code |
panoptic segmentation (2022). Si bien las
publicaciones en cuestión obtienen resultados notables por su
exactitud, llas implementaciones disponibles tienen una gran
complejidad tanto en el tamaño de los datos necesarios (modelos de
redes neurales) como en la teoría necesaria para entender su
funcionamiento. Por el contrario, en este trabajo consideramos un
algoritmo implementado en menos de 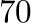 líneas de python (empleando
la librería
líneas de python (empleando
la librería numpy), basado en operaciones
algebraicas básicas, y cuyos resultados, adecuados en la gran
mayoría de las veces, sirven de línea de base para la verificación
de otros métodos.
El algoritmo presentado aquí se basa en la clasificación de puntos
en 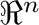 , definida
como una función
, definida
como una función
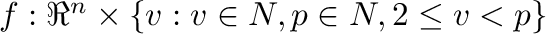 .
.
Consideremos las siguientes definiciones y convenciones:
- Una clasificación es una función que operando sobre los
elementos de un conjunto
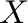 ,
les asigna a cada uno de ellos un número o rótulo de clase
,
les asigna a cada uno de ellos un número o rótulo de clase
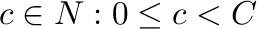 ,
donde
,
donde 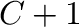 es el número total de clases (contando la clase con el rótulo 0).
es el número total de clases (contando la clase con el rótulo 0).
- Simbolizamos los vectores columnas con letras minúsculas en
negrita
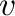 ,
y los vectores fila o transpuestos
,
y los vectores fila o transpuestos 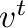 .
.
- Simbolizamos las matrices con letras mayúsculas en negrita
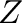 , y las
matrices transpuestas
, y las
matrices transpuestas 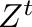 .
.
- Dada una matriz
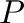 con
con 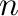 filas y
filas y  columnas,
simbolizamos sus elementos
columnas,
simbolizamos sus elementos 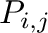 (donde
(donde
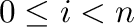 ,
,
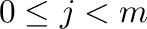 ),
y sus columnas
),
y sus columnas 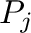 .
(Esta es la convención del índice inicial 0
para arreglos numéricos).
.
(Esta es la convención del índice inicial 0
para arreglos numéricos).
- Denotamos las matrices unitarias
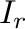 donde
donde 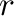 indica la
cantidad de
indica la
cantidad de 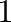 en su diagonal.
en su diagonal.
- El símbolo
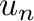 es el vector columna de
es el vector columna de 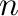 elementos iguales a
elementos iguales a 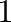 .
.
Supongamos que disponemos de  datos
datos
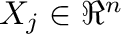 ,
y que construimos con ellos una matriz
,
y que construimos con ellos una matriz
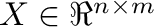 .
La descomposición en valores singulares (ver (Strang, 2016), capítulo 7) es
una operación que nos permite obtener los factores matriciales
.
La descomposición en valores singulares (ver (Strang, 2016), capítulo 7) es
una operación que nos permite obtener los factores matriciales
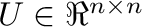 ,
,
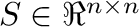 ,
,
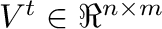 de la matriz
de la matriz
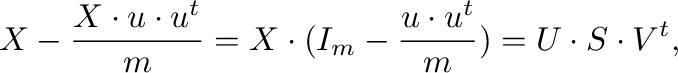 |
(1) |
donde
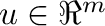 ,
,
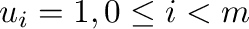 ,
e
,
e 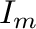 es la
matriz unitaria
es la
matriz unitaria
 .
Además,
.
Además,
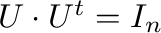 ,
,
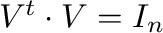 , y la matriz
, y la matriz 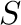 es diagonal positiva.
Observemos que el factor
es diagonal positiva.
Observemos que el factor
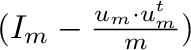 tiene al menos un autovalor
nulo, dado que
tiene al menos un autovalor
nulo, dado que
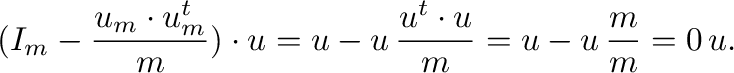 |
(2) |
Podemos construir una clasificación arbitraria de 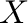 mediante los
siguientes pasos
mediante los
siguientes pasos
- Transformación de
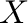 : definimos
: definimos
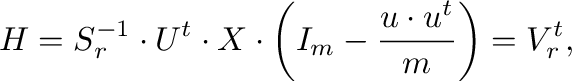 |
(3) |
donde
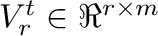 contiene las filas de
contiene las filas de 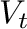 correspondientes a los
correspondientes a los 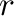 autovalores más significativos de
autovalores más significativos de 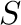 , y
, y 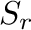 contiene los
contiene los 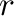 autovalores más
significativos de
autovalores más
significativos de 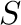 .
.
- Normalización de
 : Definimos
: Definimos 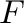 como una función
lineal de
como una función
lineal de  de forma tal que
de forma tal que
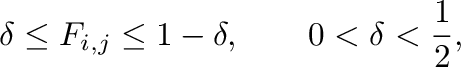 |
(4) |
 |
(5) |
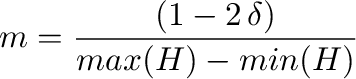 |
(6) |
y
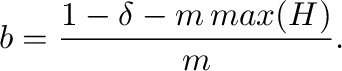 |
(7) |
- Cuantización de
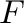 : dado un parámetro entero
: dado un parámetro entero
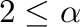 ,
calculamos los dígitos en base
,
calculamos los dígitos en base 
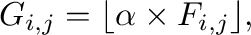 |
(8) |
donde
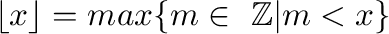 ,
, 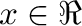 es la
función parte entera de
es la
función parte entera de 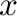 .
.
- Clasificación: finalmente calculamos los rótulos de las clases
asociadas a cada
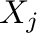 como el producto
como el producto
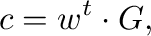 |
(9) |
donde
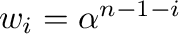 ,
para
,
para
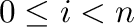 y
y
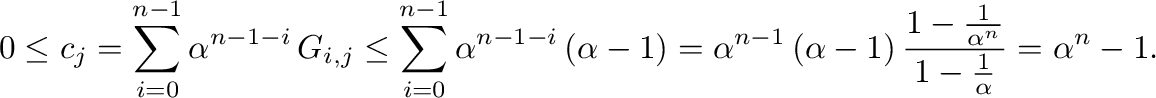 |
(10) |
El parámetro  determina la resolución de la clasificación (la cantidad de clases)
como vemos en la ecuación 10. Si bien
determina la resolución de la clasificación (la cantidad de clases)
como vemos en la ecuación 10. Si bien  puede ser cualquier
número entero mayor o igual a
puede ser cualquier
número entero mayor o igual a 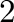 , el uso de números primos (
, el uso de números primos (
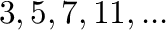 )
evita que los límites de clases de resoluciones diferentes
coincidan.
)
evita que los límites de clases de resoluciones diferentes
coincidan.
Las imágenes digitales tomadas con cámaras comerciales son
arreglos numéricos agrupados en tres o cuatro matrices, que
denominamos 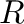 ,
,
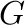 ,
, 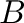 , y
, y 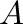 , con números
enteros positivos
, con números
enteros positivos
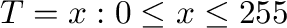 ,
de
,
de 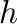 filas y
filas y 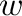 columnas. Las
matrices
columnas. Las
matrices 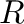 ,
,
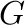 y
y 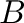 contienen
información sobre la intensidad de los colores Red (rojo), Green
(verde) y Blue (azul) que componen un punto de color o pixel.
Cuando está presente, la matriz
contienen
información sobre la intensidad de los colores Red (rojo), Green
(verde) y Blue (azul) que componen un punto de color o pixel.
Cuando está presente, la matriz 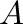 da información sobre la
transparencia del pixel.
da información sobre la
transparencia del pixel.
Definamos el pixel de la posición 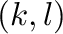 en la imagen,
en la imagen,
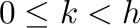 ,
,
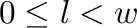 ,
como la columna
,
como la columna 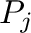 ,
,
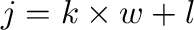
![$\displaystyle \m{P}_{j} = \left[
\begin{array}{c} R_{k, l} \\ G_{k, l} \\ B_{k, l}
\end{array} \right],$](https://www.revistas.unp.edu.ar/index.php/rediunp/article/download/849/736/2933) |
(11) |
de una matriz
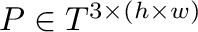 o
o
![$\displaystyle \m{P}_{j} = \left[
\begin{array}{c} R_{k, l} \\ G_{k, l} \\ B_{k, l} \\
A_{k, l}
\end{array} \right],$](https://www.revistas.unp.edu.ar/index.php/rediunp/article/download/849/736/2935) |
(12) |
de una matriz
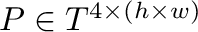 según dispongamos o no de la matriz
según dispongamos o no de la matriz 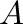 .
.
Aplicamos el algoritmo de clasificación a la matriz 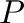 , con una
resolución
, con una
resolución
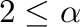 para
obtener un vector
para
obtener un vector 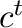 con las clases de cada columna. Dado que conociendo
con las clases de cada columna. Dado que conociendo 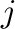 y
y 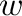 podemos calcular
podemos calcular
 |
(13) |
donde 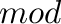 es la función que nos da el resto de la división de números enteros
es la función que nos da el resto de la división de números enteros
 , es inmediato
asignar la clase correspondiente a cada pixel de la imagen original.
Asi, podemos generar dos resultados diferentes
, es inmediato
asignar la clase correspondiente a cada pixel de la imagen original.
Asi, podemos generar dos resultados diferentes
- Mosaico: Una estructura de datos con una matriz en
![$[0, 1]^{n \times m}$](https://www.revistas.unp.edu.ar/index.php/rediunp/article/download/849/736/2942) por clase,
por clase,
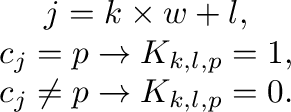 |
(14) |
- Imagen comprimida: los diferentes pixeles de cada clase son
reemplazadas por un único pixel.
Este método de segmentación es una versión modificada de los
propuestos en (Coleman y Andrews, 1979),
basados en la determinación de grupos de pixeles mediante
algoritmos de agrupamiento, según (Bell,
1966) y (Sinaga y Yang,
2020), y cuya complejidad en tiempo es NP Hard ((Mahajan ., 2009)). Dado que la
complejidad temporal de los algoritmos de cálculo de
descomposición en valores singulares es polinomial respecto al
producto de las dimensiones de la matriz, cabe esperar una mejora
en los tiempos de procesamiento (ver (X. Li
., 2019)).
La implementación y una demostración en línea del algoritmo de
segmentación está disponible en (Berns,
2022). Los programas están escritos en python, usando la
librería numpy para el cálculo de la descomposición
de valores singulares de una matriz, y la librería gradio
para la interfase web. Como se puede ver en el sitio, se puede
elegir el parámetro  ,
y el tipo de resultado (vista en mosaico, o imagen simplificada).
Se ha fijado el valor
,
y el tipo de resultado (vista en mosaico, o imagen simplificada).
Se ha fijado el valor
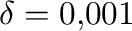 .
En la solapa con el rótulo "Files" podemos ver todos los archivos
de python con la implementación de la propuesta. Si bien la
aplicación web tal como está publicada en
.
En la solapa con el rótulo "Files" podemos ver todos los archivos
de python con la implementación de la propuesta. Si bien la
aplicación web tal como está publicada en https://huggingface.co/spaces/DWB1962/svd_codes
puede generar imágenes comprimidas, es preferible emplear el
archivo compress.py ejecutado en forma local para
una comparación justa, donde los archivos tienen el mismo formato
y la misma cantidad de pixeles.
A continuación vemos las imágenes 1,
2 y 3,
con los valores de parámetros
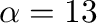 y
y
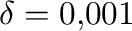 (fijo en el programa).
(fijo en el programa).
Figura 1:
Imagen original, tamaño 1654493 bytes.
|
 |
Figura 2:
Mosaico,
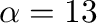 .
.
|
 |
Figura 3:
Imagen comprimida, 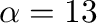 , tamaño 91498 bytes.
, tamaño 91498 bytes.
|
 |
Conclusiones
Hemos presentado un algoritmo para segmentación de imágenes,
basado en una clasificación arbitraria de pixeles determinada por
la descomposición de valores singulares de una matriz. En base a
los resultados obtenidos, es posible comprimir significativamente
una imagen en la mayoría de los casos.
Se ha publicado la implementación junto con una demostración en
línea en el sitio huggingface (ver (Berns,
2022)).
Existen algoritmos con mejor desempeño, basados en redes neurales,
cuyos artículos e implementaciones pueden consultarse en las
páginas Papers with
code | semantic segmentation (2022), Papers with code |
instance segmentation (2022) y Papers with code |
panoptic segmentation (2022). Sin embargo, creemos
que este trabajo muestra la posibilidad de obtener resultados
alternativos con programas más sencillos (en cantidad de líneas y
librerías usadas).
Badrinarayanan, V., Kendall, A., y Cipolla, R. (2017). Segnet: A
deep convolutional encoder-
decoder architecture for image segmentation. IEEE transactions on
pattern analysis and machine
intelligence, 39 (12), 2481–2495.
Bell, G. H. (1966). A comparison of some cluster-seeking techniques.
(Inf. Téc.). STANFORD
RESEARCH INST MENLO PARK CALIF.
Berns, D. W. (2022). Huggingface | svdcodes. https://bit.ly/3gMAWO7.
((último acceso en
2022-10-25))
Beucher, S. (1992). The watershed transformation applied to image
segmentation. Scanning
Microscopy, 1992 (6), 28.
Cheriet, M., Said, J. N., y Suen, C. Y. (1998). A recursive
thresholding technique for image
segmentation. IEEE transactions on image processing, 7 (6), 918–921.
Coleman, G. B., y Andrews, H. C. (1979). Image segmentation by
clustering. Proceedings of the
IEEE, 67 (5), 773–785.
Jurado, J. M., López, A., Pádua, L., y Sousa, J. J. (2022). Remote
sensing image fusion on 3d scenarios: A review of applications for
agriculture and forestry. International Journal of Applied
Earth Observation and Geoinformation, 112 , 102856. Descargado
de
https://www.sciencedirect.com/science/article/pii/S1569843222000589
doi: https://doi.org/10.1016/j.jag.2022.102856
Ke, L., Tai, Y.-W., y Tang, C.-K. (2021). Deep occlusion-aware
instance segmentation with overlap-
ping bilayers. En Proceedings of the ieee/cvf conference on computer
vision and pattern recognition (pp. 4019–4028).
Kirillov, A., He, K., Girshick, R., Rother, C., y Dollár, P. (2019).
Panoptic segmentation. En
Proceedings of the ieee/cvf conference on computer vision and
pattern recognition (pp. 9404–
9413).
Kotaridis, I., y Lazaridou, M. (2021). Remote sensing image
segmentation advances: A meta-
analysis. ISPRS Journal of Photogrammetry and Remote Sensing, 173 ,
309–322.
Li, L., Qian, B., Lian, J., Zheng, W., y Zhou, Y. (2018). Traffic
scene segmentation based on rgb-
d image and deep learning. IEEE Transactions on Intelligent
Transportation Systems, 19 (5),
1664-1669. doi: 10.1109/TITS.2017.2724138
Li, X., Wang, S., y Cai, Y. (2019). Tutorial: Complexity analysis of
singular value decomposition
and its variants. arXiv preprint arXiv:1906.12085 .
Liu, X., Song, L., Liu, S., y Zhang, Y. (2021). A review of
deep-learning-based medical image
segmentation methods. Sustainability, 13 (3), 1224.
Mahajan, M., Nimbhorkar, P., y Varadarajan, K. (2009). The planar
k-means problem is np-hard.
En International workshop on algorithms and computation (pp.
274–285).
Minaee, S., Boykov, Y. Y., Porikli, F., Plaza, A. J., Kehtarnavaz,
N., y Terzopoulos, D. (2021).
Image segmentation using deep learning: A survey. IEEE transactions
on pattern analysis and
machine intelligence.
Muthukrishnan, R., y Radha, M. (2011). Edge detection techniques for
image segmentation.
International Journal of Computer Science & Information
Technology, 3 (6), 259.
Papadeas, I., Tsochatzidis, L., Amanatiadis, A., y Pratikakis, I.
(2021). Real-time semantic image
segmentation with deep learning for autonomous driving: A survey.
Applied Sciences, 11 (19),
8802.
Papers with code | image segmentation. (2022).
https://bit.ly/3sBdNkp. ((último acceso en
2022-10-25))
Papers with code | instance segmentation. (2022).
https://bit.ly/3TXr1Dx. ((último acceso en
2022-10-25))
Papers with code | panoptic segmentation. (2022).
https://bit.ly/3SUayzn. ((último acceso en
2022-10-25))
Papers with code | semantic segmentation. (2022).
https://bit.ly/3N9lho4. ((último acceso en
2022-10-25))
Ramesh, K., Kumar, G. K., Swapna, K., Datta, D., y Rajest, S. S.
(2021). A review of medical image segmentation algorithms. EAI
Endorsed Transactions on Pervasive Health and Technology,
7 (27), e6–e6.
Ren, M., y Zemel, R. S. (2017, July). End-to-end instance
segmentation with recurrent attention.
En Proceedings of the ieee conference on computer vision and pattern
recognition (cvpr).
Ronneberger, O., Fischer, P., y Brox, T. (2015). U-net:
Convolutional networks for biomedical image
segmentation. En International conference on medical image computing
and computer-assisted
intervention (pp. 234–241).
Shih, F. Y., y Cheng, S. (2005). Automatic seeded region growing for
color image segmentation.
Image and vision computing, 23 (10), 877–886.
Sinaga, K. P., y Yang, M.-S. (2020). Unsupervised k-means clustering
algorithm. IEEE access, 8 ,
80716–80727.
Strang, G. (2016). Introduction to linear algebra.
Wellesley-Cambridge Press. Descargado de
https://books.google.com.ar/books?id=efbxjwEACAAJ
Treml, M., Arjona-Medina, J., Unterthiner, T., Durgesh, R.,
Friedmann, F., Schuberth, P., . . .
others (2016). Speeding up semantic segmentation for autonomous
driving.
Wang, W., Bao, H., Dong, L., Bjorck, J., Peng, Z., Liu, Q., . . .
others (2022). Image as a foreign lan-
guage: Beit pretraining for all vision and vision-language tasks.
arXiv preprint arXiv:2208.10442 .
Waqas Zamir, S., Arora, A., Gupta, A., Khan, S., Sun, G., Shahbaz
Khan, F., . . . Bai, X. (2019).
isaid: A large-scale dataset for instance segmentation in aerial
images. En Proceedings of the
ieee/cvf conference on computer vision and pattern recognition
workshops (pp. 28–37).
Wei, Y., Hu, H., Xie, Z., Zhang, Z., Cao, Y., Bao, J., . . . Guo, B.
(2022). Contrastive learning rivals
masked image modeling in fine-tuning via feature distillation. arXiv
preprint arXiv:2205.14141 .
Xiong, Y., Liao, R., Zhao, H., Hu, R., Bai, M., Yumer, E., y
Urtasun, R. (2019). Upsnet: A unified
panoptic segmentation network. En Proceedings of the ieee/cvf
conference on computer vision
and pattern recognition (pp. 8818–8826).